路昌工業股份有限公司

第一章：轉移函數 Transfer Function

轉移函數，係指以數學表示式描述一現象時，其現象的輸入因素與輸出結果之間的數學關係式。如數學式y = ax，其中y可視為輸出，x視為輸入，則y/x = a，則a為輸出y與輸入x之間的數學關係式，即為控制系統中的轉移函數。 

1-1   控制系統概論

一個完整的控制系統(Control_System)需含有兩個基本架構，即為受控系統(System)及控制器(Controller)。若以輸出回授(Feedback)功能具備與否區別，可分為開迴路(Open-loop_Control_System)及閉迴路控制系統(Closed-loop_Control_System)，如圖1-1，其中r表示控制命令(Command)，u為系統輸入訊號(Input)，y為系統輸出訊號(Output)，b是回授訊號，e是誤差訊號(Error)。

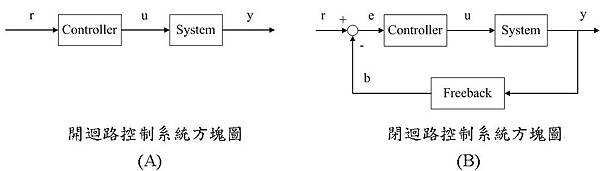
圖1-1：控制系統方塊圖 

由圖1-1可知，開迴路控制系統是給定控制命令後，經由控制器轉換成相對應的輸入訊號進入系統中，預估系統輸出訊號能達到控制命令的目標值。此種方式適用於系統輸入與輸出之間的關係為已知且可靠的，同時無嚴重的外部干擾下使用，具有簡單及經濟的使用特徵，適合用於準確度要求不高及低成本的場合。

閉迴路控制系統則會將系統輸出訊號進行回授，與控制命令訊號進行比較，產生誤差訊號以修正系統輸入訊號，達到控制命令目標需求。此方法可有效提高系統準確度並降低外部雜訊干擾，具有誤差自動修補效果；圖1-2中，開迴路控制系統遇到非預期之外部負載發生，將導致系統輸出無法達到目標值；而閉迴路系統則可自動修正誤差達到輸出目標值。

圖1-2：系統響應圖 

控制系統之目的，係有效規劃控制器，驅使受控制系統達到預期輸出目標；有鑑於此，分析受控系統為有效控制的第一步驟，先確認受控系統可控性、操作範圍、穩定度、靈敏度及精確度等相關參數，才可設計相對應的控制器規格與模式，得到準確且有效的控制輸出結果。以較為生活化的例子進行說明，對於一名參加馬拉松比賽的選手，最終目標是以最短時間內到達終點贏得比賽(可視為輸入命令目標)，故須於賽前了解比賽相關資訊(系統)，如比賽路程、地面狀況及對手情報等相關資訊，藉此調整賽跑的速度及體力的消耗等(控制器調整)，以達到最佳的比賽策略並贏得比賽 (輸出結果)。

圖1-3為受控系統，簡稱為系統，以符號G表示，泛指一種可接受某一形式之能量輸入，而產生相對應之輸出反應的行為或物質。以種田為例，可視為輸入水與養份，所收穫之稻米為輸出，則種田也可視為一種系統；然而，此一名詞大多用於物理相關領域之中，如機械結構、電子電路及化工程序等。若以數學方程式表示，輸入、輸出與系統之間的關係可寫成y = G[u]。

圖1-3：系統方塊圖 

系統所包含的範圍十分廣闊，然而並非所有的系統皆可達到預期的控制效果，甚至有不受控制的系統。故需先將系統依其特性分類，規範出可穩定控制之系統所須具備的條件。於控制系統中，將系統性質分為四項以進行可控性評估，分別為鬆弛系統(Relaxed_System)、線性系統(Linear_System)、非時變系統(Time-Invariant System)及因果系統(Causal_System)。 

    1.鬆弛系統

係指該系統並未具有自發性的能量存在，且為不儲存能量之物理系統，其定義系統在某一時間點t=t₀上的初始值(Initial_Condition)為零，即無輸入且無輸出，系統之輸入與輸出滿足下列條件。一般而言，任何系統在時間為負無限大時，均視為鬆弛系統。

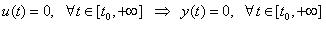
    2.線性系統

係指輸入與輸出之間成比例關係的系統，其曲線為通過原點之直線，如圖1-4。線性系統且符合下列之重疊定理。

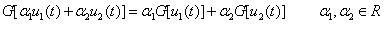
嚴格來說，線性系統是不存在的，任何物理系統皆具有部份非線性區間，如飽和(Saturation)、死帶(Dead_Zone)、齒隙(Backlash)及遲滯(Hyteresis)等情況。然而非線性(Nonlinear)的存在，使得系統分析與設計複雜化，故將系統操作於線性區內或假定系統為多段式線性化，皆為常見之簡化方式。

圖1-4：線性系統 

    3.非時變系統

系統特性不隨時間而改變，其輸入與輸出關係將滿足下列條件，其中τ表示延遲時間。

參考圖1-5，(A)為原系統之響應，(B)是經過時間延遲τ後系統之響應，除了時間變化外，其餘特性皆未改變。事實上，所有的物質特性皆會受到時間的影響而變化，如壽命及衰減的問題，但需經過一段較長的時間之後才會受到影響，遠大於操作時間，故可視為非時變系統。

圖1-5：非時變系統 

    4.因果系統

系統現在的輸出結果，僅受到現在或過去的輸入所影響，而與將來的輸入無關。因果系統為一般的物理現象所具備的；圖1-6為非因果系統，在未輸入的情況下，已具有輸出結果。

圖1-6：非因果系統

經由上述之系統性質分析後，將一個實際的物理系統，針對所需之輸入與輸出的物理關係建立成模型(Model)，以數學化的方式進行系統描述；這種利用系統輸入及輸出關係求轉移函數之過程，稱為系統建模(System_Modeling)。

一般的控制系統建模可分為兩種區域性(Domain)，分別為時域(Time-domain)及頻域(Spatial-domain)，另外還有三種不同的表示型態，轉移函數(Transfer_Function)、極零點增益公式(Zero-Pole_Gain_Formula)及狀態空間(State_Space)。 

時域：是描述數學函數或物理信號對時間的關係，例如一個信號之時域波形可表達信號隨著時間的變化情況，自然界中的一切行為皆與時間有關係。 

頻域：時域函數經由拉式轉換(Laplace_Transform)後，稱為頻域函數，是描述數學函數或系統特性針對空間頻率的關係，例如一個系統的頻率圖型可以代表系統在不同工作頻率下所表現之響應特性。 

        1. 轉移函數：頻域

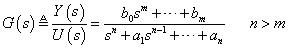
其定義如下：

一個線性非時變之系統，由其物理特性可推得代表系統之動態微分方程式

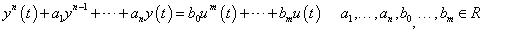
其中y(t)為系統輸出，u(t)為系統輸入。

令系統於時間t=0之初始值為零，亦即

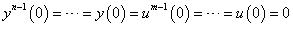
將其進行拉氏轉換，並定義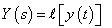及    

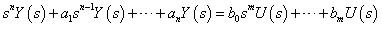
整理之後可求得轉移函數

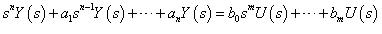
例：

求系統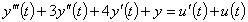 之轉移函數。

解：

對系統微分方程取拉氏轉換，並令初始值為零，則可得到系統之轉移函數

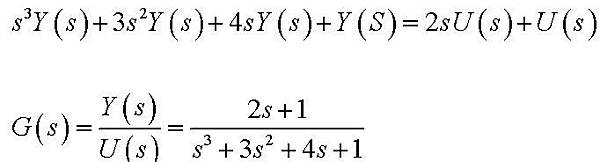
        2. 極零點增益公式：頻域

為轉移函數之特別表示式：

其中：

s = －z₁，…，－z_m  稱為系統零點（Zero）

s = －p₁，…，－p_n  稱為系統零點（Pole）

K 稱為系統增益常數（Gain Constant） 

        3. 狀態空間：時域

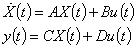
是用來描述一個具有多個輸入u、多個輸出y及多個變數X的系統，將其狀態變數的微分表示成所有狀態與輸入之線性關係組合。 

其定義如下：

其系統之描述是用所需之最少的狀態變數(x₁,x₂,…,x_n)，且加入的輸入訊號係根據狀態變數在時間t₀的值(即變數的初始值)，便足夠決定系統在t≧t₀的狀態行為所表示的一階微分方程式，此一階微分方程式的一般形式如下

將上述方程式以矩陣型式改寫如下

以向量表示狀態變數X，輸入訊號向量定義為u，可將系統的狀態微分方程式(State Differential Equation)，以簡潔符號寫成

狀態微分方程式為狀態變數與系統狀態及輸入訊號之間的關係式，而系統輸出訊號與狀態變數及輸入訊號之間的關係式，即為輸出方程式(Output_Equation) 

y是以向量形式表示的輸出訊號 

事實上，轉移函數與極零點增益公式是相同的，將轉移函數以極零點增益公式表示有助於系統特性分析及使用。而狀態空間與轉移函數之間的關係，可利用拉式轉換求得如下：

其詳細說明如下，先假設系統的動態方程式為：

將其取拉氏轉換，並令初始值X（0）=0，則可得：

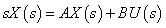                                    (1-1)

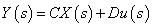                                      (1-2)

由式(1-1)可得  ，代入式(1-2)：

所以：

描述系統之數學模型比較：

求得系統轉移函數後，才能由轉移函數對系統做明確的分析，並進一步得知系統在不同型式命令下之響應。 

1-2   自動控制數學基礎

自動控制常用之基本函數：

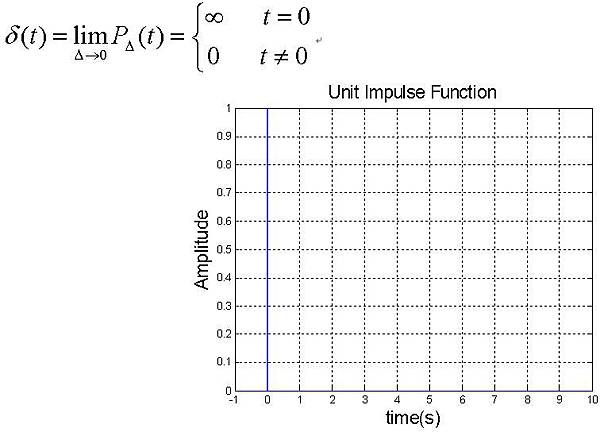
        1. 單位脈衝函數(Unit Impulse Function)

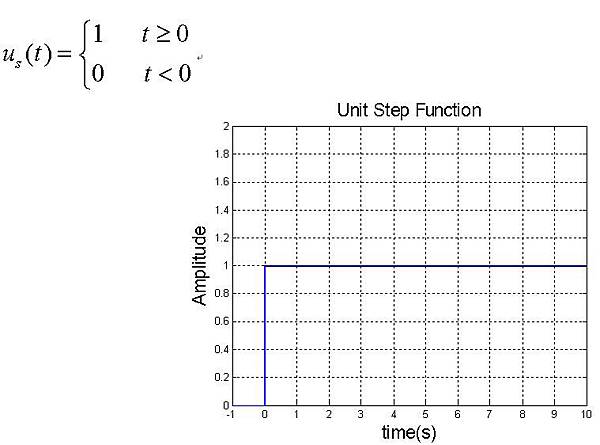
        2. 單位步階函數(Unit Step Function)

        3. 單位斜坡函數(Unit Ramp Function)

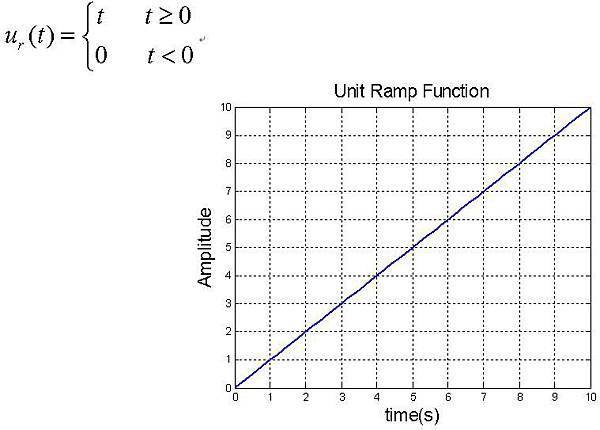
        4. 單位拋物線函數(Unit Parabolic Function)

        5. 延遲函數(Delay Function)

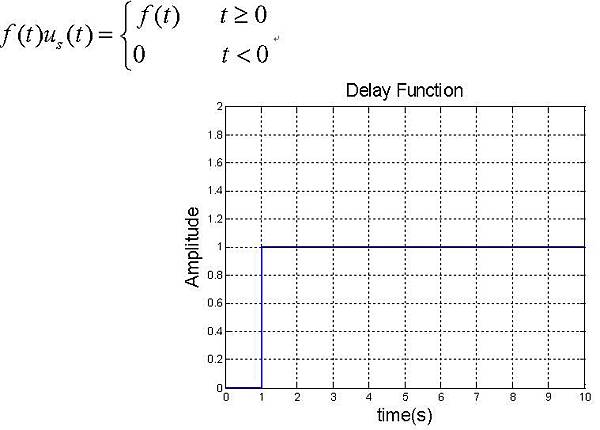
各函數之間的關係式如下

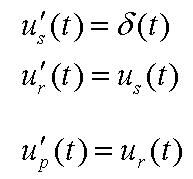
拉氏轉換：

拉普拉斯轉換，簡稱拉氏轉換，能求得實際系統的線性近似模型，以代數方程式取代較難求解的微分方程式；系統之時間響應解可由下列運算步驟獲得:

1. 求得系統微分方程式
2. 得出微分方程式的拉普拉斯解
3. 解變數經轉換的代數方程式 

其定義如下：

於函數f(t)的拉氏轉換，只有在拉普拉斯積分是收斂的情況下才存在；即為f(t)必須是在對於t > 0的每一個有限區間內都是片斷性連續的，且當t趨於無窮大的時候，f(t)是呈現指數階變化。 

若f(t)為可拉氏轉換，對某正實數，則下式成立

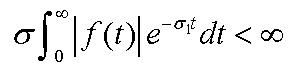
於t > 0時，︱f(t)︱< Me^αt，則當  時，此積分將會收斂，其收斂區域為  ，而  為絕對收斂之橫座標；一般的物理訊號皆符合此條件。 

已知函數f(t)可拉氏轉換，且當t < 0時，f(t)=0，即

對於某個有限的實數σ，其拉式轉換為

其反拉氏轉換(Inverse Laplace Transform)為

常用之拉氏轉換：

1-3 電路系統求解轉移函數

在處理工程問題時，常將各種物理現象以電路元件表示，以方便分析、模擬及求解，如熱力學中各材料之熱阻及熱容，機械系統中的各種阻尼及慣量，都轉換為電子元件中的電阻及電容表示，則可求解電路系統之轉移函數即為物理系統輸入與輸出之間的關係；以下將簡介從電路系統求解轉移函數之流程。

例：

由下列之電路系統進行轉移函數求解：

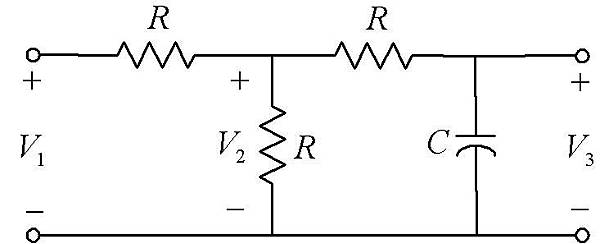
圖1-7：電子電路系統

以電路觀點求解：

電路元件中的組成，不外乎串聯及並聯兩種方式，而所有的元件皆可視為電阻來進行計算，故V₃與V₁之關係可用電阻分壓的計算方式求得。

電阻串聯分壓 

圖1-8：串聯電路

電阻並聯分壓 

圖1-9：並聯電路

則圖1-7中的電路可直接求得

以自動控制觀點求解：

此電路之輸入端為V₁，輸出端為V₃，則轉移函數可表示為：

先令此一系統之狀態時間趨近無窮遠處，則其拉式轉換之頻域s會趨近於零，此時電路圖上之電容等同開路作用；令s=0且V₃=V₂則可求得K值： 

圖1-10：時間趨近無窮，電容開路

第二步驟，假設輸出端短路(  )，計算所流入的電流值大小即為；因路徑上無任何電阻，故流入電流值為零。 

圖1-11：求解V₃短路後，其路徑上通過之電流值

最後假設輸入端短路(  )，即可得到   

圖1-12：求解V₁短路後，其路徑上通過之電流值

則系統之轉移函數可求得

1-4   梅森增益公式 Mason Gain Formula

Samuel_Jefferson_Mason於西元1953年，在IEEE上發表了一篇文章Feedback_Theory-Some_Properties_of_Signal_Flow_Graphs，其內容探討信號流程圖(Signal_Flow_Graph)處理與特徵，之後演變為自動控制中常使用的梅森增益公式，或稱為梅森法則(Mason’s_Rule)。

此篇文章中大多係描述信號流程圖的簡化處理，如同Mason所秉持的研究方法：「當求解一個困難的問題時，先集中注意力去分析其中較為容易的部份，而困難的部份也會隨之解開。」將複雜的信號流程圖，拆解為較小且簡易的部份先進行研究分析，將閉迴路體系統分解成容易處理之開迴路系統，如圖1-13，待個別特徵分析完成後，再重新組合以求得總體系統之解答。

圖1-13：信號流程圖拆解

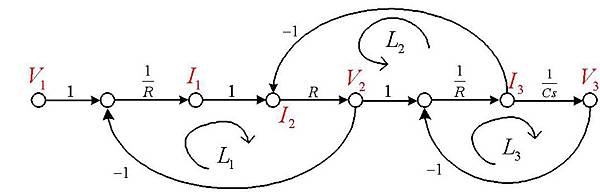
圖1-14：信號流程圖

圖1-14即為圖1-7中之電路所轉換的信號流程圖，則系統之輸入與輸出之間的關係，可直接用梅森增益公式求得；其公式說明如下：

M = 輸入與輸出間的轉移函數

y_out = 輸出節點(node)的變數

y_in  = 輸入節點的變數

M_k  = 執行路徑之增益(Gain)

N = 前進路徑總數

△ = 1-(所有迴路增益的和)+(所有兩個未接觸的迴路增益乘積的和)

　  -(所有三個未接觸的迴路增益乘積的和)

+(所有四個未接觸的迴路增益乘積的和)……

△_k = 與第k個前進路徑不接觸的迴路所求得的△ 

此流程圖具有下列三個迴圈(Loop)路徑：

又，此流程圖之所有迴圈路徑皆與主路徑相接觸，而L₁及L₃之間無接觸，則此一系統之轉移函數為：

其結果與使用電路方式求解相同。

 1-5   線性分式轉換 Linear_Fractional_Transformation

隨著科技文明的持續演進，各類複雜的數學運算大多交由電腦進行處理，同時為了增加電腦的運算速度，矩陣計算被大量運用於電腦資料處理之中；於系統控制與分析時，同樣地將系統表示成矩陣之形式，以加快電腦進行運算處理，因此，以狀態空間對控制系統進行描述的方式，基於其利用矩陣運算的便利性，以及可用以描述多輸入多輸出的特質，在後現代控制中，儼然取代了傳統的控制描述方式，成為了新的主流。

另一方面，為了同時配合矩陣運算時所提出的各項法則以及描述上的便利性，源於電子電路的雙端網路(Two_Port_Network)架構提供了一個矩陣型態的良好表示，如圖1-15，這樣的描述架構根據所定義的輸入及輸出不同，又可細分為H參數，Y參數，Z參數，T參數等等；而將矩陣及雙端網路概念完整結合，並發展為控制系統所使用之型式，則稱為線性分式轉換(Linear_Fractional_Transformation)。

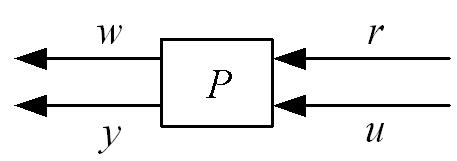
圖1-15：雙端網路方塊圖

圖1-16為線性分式轉換方塊圖，將原本圖1-1的控制系統方塊圖之單輸入單輸出系統，轉換為多輸入多輸出的表示，其中P為系統，k為控制器；雖然此方塊圖僅僅是改變了控制器的擺設方式及位置，但從物理系統的觀點來看，控制器除了原本的外部輸入控制之外，還包括了直接改變系統物理特性的解釋，如同化學中的添加劑、機械材料的熱處理及塑膠材料的混合等，加入了一種外部的處理或是成份，導致系統特性的改變，使其輸入與輸出的特徵產生變化，可用於更廣泛之系統描述。

圖1-16：線性分式轉換方塊圖

轉移函數推導如下：

LFT系統描述

將(1-3)矩陣展開

(1-4)可推導為

將(1-4)及(1-7)代入(1-5)中

LFT系統求解方式：

以圖1-7之系統為例，先將其轉為控制系統方塊圖，如圖1-17，再依照以下的步驟求解。

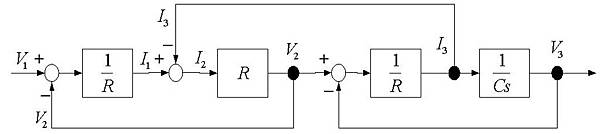
圖1-17：控制系統方塊圖

步驟一：

將此系統修改成雙端網路的表示模式，其實際作法係將系統拆解為多段之開迴路系統，將原系統的閉迴路連結路徑全部斷開，可稱之為剪刀法，則可將系統劃分為兩部份，改寫成雙端網路型式，則控制器之增益為原閉迴路之增益，如圖1-18。圖1-19為較理想之剪斷的模式，係以最少的剪斷點，達到無閉迴路路徑之結果；為了確保剪斷後的系統為開迴路系統，可於各閉迴路路徑增加剪斷點，但每多增加一個剪斷點即多一組輸出及輸入變數，將使得系統之P矩陣越為龐大，運算上會較為費時，故剪斷點越少越好。

圖1-18：單端網路改為雙端網路

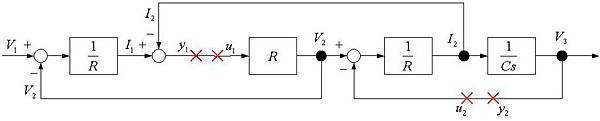
圖1-19：將閉迴路系統剪斷為多段的開迴路系統

步驟二：

由圖1-19可知，此系統具有兩個剪斷點，故共有三組輸入(V₁,u₁,u₂)及輸出(V₃,y₁,y₂)端點，則其個別之轉移函數共具有9組，如下所示

以矩陣型式表示如下，即為此系統之轉移函數P

又，此系統控制器k之轉移函數，即為斷開點之輸入(u₁,u₂)與輸出間(y₁,y₂)之增益值，由圖1-19可知為1，為配合矩陣運算，故以單位矩陣表示

步驟三：

將系統P及控制器k參數代入公式(1-8)中計算，則此系統之轉移函數可得。

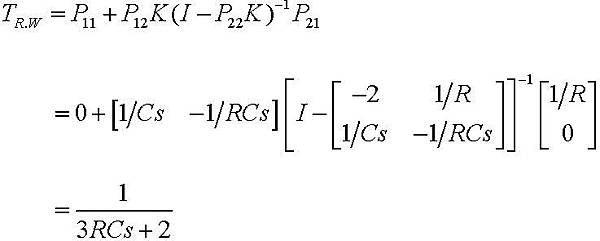
1-6   總結

本章節說明了轉移函數於控制系統中所扮演的角色，並解釋其表示的型態與類型，如時域、頻域與極零點等相關描述方式。事實上，轉移函數即代表控制系統中的系統行為模式與規則，故求解出系統轉移函數，即可對系統進行有效的分析及控制；本章介紹了四種求解轉移函數的方式，供使用者參考，分別從電路及控制方法求解，或套用梅森增益法則，以及適合應用於多輸入輸出系統的線性分式轉換法。

隨著電腦運算速度的發展，單輸入輸出模式的處理速度已經到達瓶頸，為了得到更快的處理速度及效率，多通道的多輸入輸出模式已經成為電腦相關產業的主流，如多核心電腦。自動控制的發展也如同電腦科技一般，由單輸入輸出的古典控制持續演進到多輸入輸出的近代控制；近幾年來，自動控制技術與電腦科技更加緊密的結合後，發展出更完善的多輸入輸出控制法則，稱為後現代控制，線性分式轉換法即為後現代控制理論中所發展出的轉移函數求解方式。有鑑於此，下一章將針對多輸入輸出的後現代控制理論進行深入探討。

路昌工業網站：http://lutron-ind.weebly.com/