第二章：多輸入輸出(MIMO)系統
系統可同時接受多組輸入而產生相對應的輸出，即為多輸入輸出系統；一般真實的系統輸入變數往往不只一個，且都會影響到輸出結果，如馬達，其輸入包括電壓及電流等變數，而會造成輸出轉速及轉矩的變化。多輸入輸出系統是接近真實狀態的描述，也與目前的科技發展趨勢一致，故於本章節做更詳細的介紹。
2-1 動態方程式
動態方程式(Dynamic_Equation)是用來描述一個多輸入(uj)輸出(yq)的多變數(xn)系統，將其狀態變數的微分表示成所有狀態與輸入之組合關係。
於自動控制系統中，決定系統的動態方程式，需先定義系統所需之最少變數，如x1(t)，x2(t)，…xn(t)，並加入的輸入訊號根據變數在時間t0的值，即變數的初始值；最終決定系統在t≧t0之狀態行為動態方程式，分為兩組方程式表示，狀態方程式及輸出方程式：
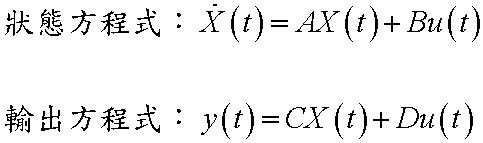
系統動態方程式即為自動控制中轉移函數的狀態空間表示形態。然而，一般而言轉移函數僅適用線性非時變(LTI)系統，而動態方程式的優點在於可以表達任一系統，如
1.線性非時變系統 (Linear&Time-Invariant System)
2.線性時變系統(Linear&Time-Variant System)
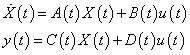
3.非線性非時變系統(Nonlinear&Time-Invariant System)
4.非線性時變系統(Nonlinear&Time-Variant System)
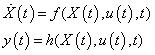
2-2 轉移函數分解為動態方程式之方法與解析
於第一章中有介紹狀態空間轉成轉移函數的推導，本章節則將介紹由轉移函數改成多輸入輸出之動態方程式的作法。
1.直接分解法(Direct_Decomposition)
將轉移函式改寫成為下面的形式，其中L(s)為輔助狀態方程式
步驟一：定義狀態變數 x1，x2，…xn
狀態變數的數量即等於轉移函數的階層，使用下述系統輸出及輸入方程式作為範例說明。
經由反拉氏(Inverse_Laplace)轉換後可改寫為
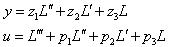
則定義此系統的狀態變數為
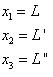
步驟二：動態方程式的建構
令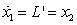
及
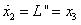，則系統動態方程式可編寫如下：
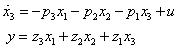
步驟三：動態方程式的矩陣結構
將動態方程式以矩陣型式排列：
例一：利用直接分解法描述轉移函數之動態方程式。
解：先將轉移函數分解為輸入及輸出方程式
做反拉式轉換可得
定義狀態變數
則此系統動態方程式為
經由之前的步驟可求得其動態方程式矩陣形態為
<觀察>
將原來的轉移函數改成升冪的方式排列如下
則A矩陣的最後一列由分母係數決定且均變號，C列向量由分子係數來決定，可更快求得轉移函數之動態方程式。
二.巢狀分解法(Nested_Decomposition)
將轉移函數改寫如下
步驟一：定義狀態變數 x1，x2，…xn
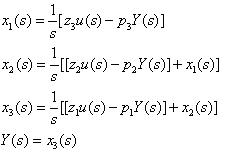
步驟二：動態方程式的建構
步驟三：動態方程式的矩陣結構
例二：利用巢狀分解法描述轉移函數的動態方程式。
解：由於轉移函數並非嚴格真分有理函數故改寫為
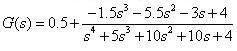
此轉移函數為四階，利用上述步驟加上原矩陣之增廣矩陣找出動態方程式
<觀察>
從矩陣的元素可發現，其轉移矩陣和狀態方程式的分母和分子係數，具有一定的相關性。
<補充>
用直接分解法來解決問題，可發現當D項有值時，會造成轉移函數變為真分有理函數。
三.串聯分解法(Cascade_Decomposition)
串聯分解法名稱的由來，係因其所繪製的訊號流程圖為串聯式結構。首先，先將轉移函數因式分解為下列形式
再將因式分解過後的轉移函數以訊號流程圖表示，其中訊號流程的實現有以下兩個基本圖例：
1.
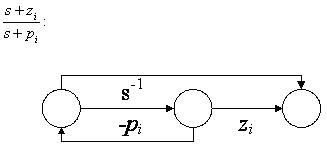
圖2-1：流程圖
2.
圖2-2：流程圖
以下以實例說明。
例三：利用串聯分解法描述轉移數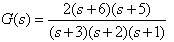
的動態方程式
解：將轉移函數分解如下
步驟一：實現流程圖
圖2-3：串聯式流程圖
步驟二：動態方程式的建構
步驟三：動態方程式的矩陣結構
<觀察>
1.由於定義狀態的不同以及建構訊號流程圖的方法有無限多種，故使用此法答案並不唯一。
2.串聯分解法的形式必為三角矩陣，而其三角矩陣之對角元素即為轉移函數的極點(pole)位置。
四.並聯分解法(Cascade_Decomposition)
與串聯分解法類似，其訊號流程圖為並聯式結構。同樣，先將轉移函數因式分解為下列形式
步驟一：實現流程圖
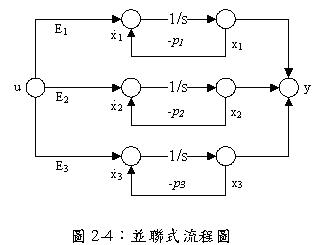
步驟二：動態方程式的建構
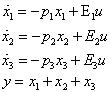
步驟三：動態方程式的矩陣結構
<觀察>
1.由於定義狀態的不同以及建構訊號流程圖的方法有無限多種，故使用此法答案並不唯一。
2.並聯分解法的A矩陣為對角矩陣或者是Jordan矩陣，其對角線元素即為其部份分式的極點(Pole)位置。
<特別討論>
若G(s)發生重根的現象,例如
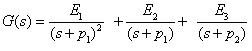
則訊號流程圖定義狀態為
其動態方程式為
上述介紹了四種由轉移函數改為動態方程式表示式，可發現動態方程式結果並不唯一；因此，從原始的系統狀態來分析一個系統其動態方程式的可能性，是否並不唯一。考慮一系統如下
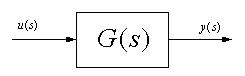
圖2-6：控制系統圖
其狀態空間表示式為
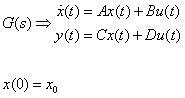
其流程圖如下
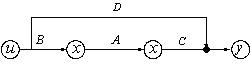
圖2-7：狀態流程圖
則必定存在任一非奇異矩陣(Nonsingular Matrix) P，使得系統參數可以轉換
其轉換方式可參考下圖
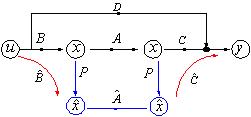
圖2-8：轉換狀態流程圖
其中
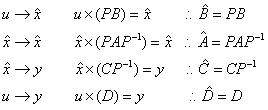
則其狀態空間表示式可改寫為
因非奇異矩陣並不唯一，具有無窮多種可能性，故造成同樣的系統可有無窮多種的動態方程表示式。
2-3 線性分式轉換探討
由第一章可知，線性分式轉換是專門處理多輸入輸出型式的轉移函數求解方法，而一般的線性分式轉換雙端網路型式如圖2-10所示，其方程式描述如下。
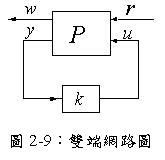
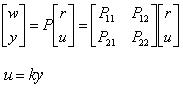
由第一章的推導可知其轉移函數為
若以動態方程式表示，則
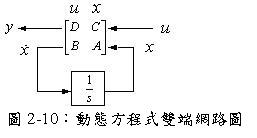
轉移函數應寫成
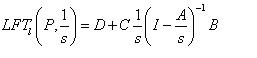
也可將系統參數k至於P上方的位置，為另一型式的雙端網路，如圖2-11所示，則其轉移函數求解公式也會有所變化。
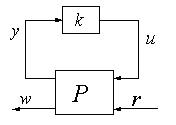
圖2-11：雙端網路圖
轉移函數推導如下
以動態方程式表示其型式，則
圖2-12：動態方程式雙端網路圖
轉移函數為
除了上述不同型態的雙端網路之外，以下將針對不同樣式之系統，各別講解採用線性分式轉換求解之方法及解析。
型式一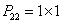
：，系統流程如圖2-13所示
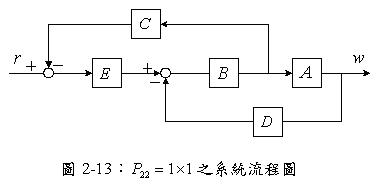
加入一斷開點，使得輸入至輸出為開迴路路徑，如下圖2-14所示
將各別輸入與輸出間之關係加以排列，可得
以動態方程式雙端網路圖表示如下
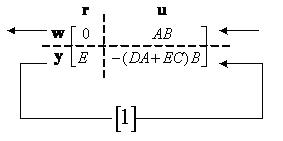
圖2-15：動態方程式雙端網路圖
代入線性分式轉換可得
型式二：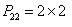
，系統流程如圖2-16所示
加入斷開點，使得輸入至輸出為開迴路路徑，如下圖2-17所示
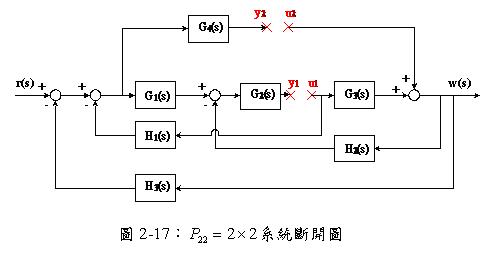
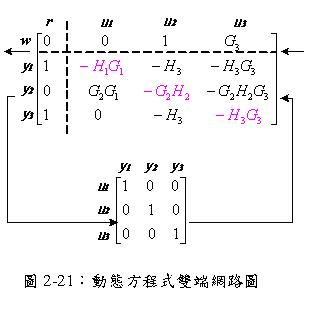
將各別輸入與輸出間之關係加以排列，並以動態方程式雙端網路圖表示如下
代入線性分式轉換可得
加入斷開點，使得輸入至輸出為開迴路路徑，如下圖2-20所示
將各別輸入與輸出間之關係加以排列，並以動態方程式雙端網路圖表示如下
代入線性分式轉換可得
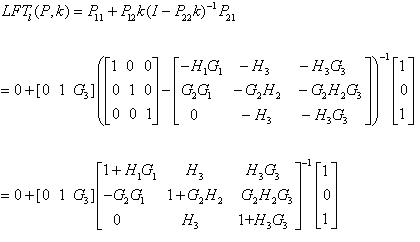
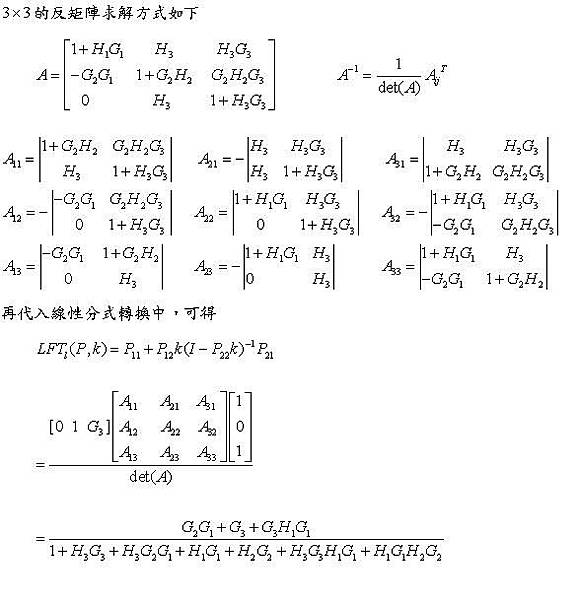
由上述可知，斷開點的數量會影響於矩陣之大小，越大則計算上會越為複雜，因此，盡可能以最少的切斷點來完成開回路系統，以避免計算上的困難。
2-4 總結
本章節介紹了用來描述多輸入輸出系統之動態方程式及其相關特性，並推導不同類型的動態方程式及轉移函數間轉換之方法。而方便用於多輸入輸出系統求轉移函數的線性分式轉換，具有不同的系統表示型式，而造成求解方程式之差異性；本章節也以線性分式轉換求解更為複雜且龐大的系統，分析其解法與流程及產生的影響。
經由本章節的介紹可明顯的發現，無論是動態方程式或是線性分式轉換，皆是以矩陣的型式表式，而矩陣的運算對於人的運算是較為複雜且不便的，但若以電腦進行求解時，卻能大幅的提高計算的時效性，因此在實際的應用領域當中，以矩陣表示是較為恰當的，極為後現代控制理論發展的主軸。
留言列表
{{ article.title }}
馬達科技產品介紹 (1)