第三章:運算放大器(OP-AMP)
經由前述章節之介紹,可知轉移函數於系統中之重要性,但如何將一個實際的系統情況真實的表現出來,也是一個研究的重點,除了直接觀察系統本身行為之外,最常用來表達真實表現系統狀態的,即為電子電路裝置,利用電子零件,如電阻、電容及電感來表示相對應的物理系統,但其中還需要一個關鍵零件,即為運算放大器(Operational_Amplifier,簡稱OP、OPA或OP-AMP),以達到使用電子電路裝置模擬系統行為表現。故本章節將詳細介紹運算放大器及其於控制系統中的模擬應用方法。
3-1運算放大器簡介
運算放大器,如圖3-1,係一種具有雙端差動輸入及單端高增益(Gain)輸出的電壓放大器,可將輸入的兩端電壓差經過增益後輸出,其輸入與輸出關係之數學表示式如下:
Vout=A0(V+ - V-)
其中A0為運算放大器之內部電壓增益(Open-loop_Voltage_Gain),其實際增益值約為104 ~ 106。

理想的運算放大器,需具備以下幾個特點
1.無限大的輸入阻抗(rin=∞):理想的運算放大器輸入端不容許任何電流流入,即上圖中的V+與V-端點的電流值為零,代表輸入阻抗無限大,然實際電路之阻抗值約為106 Ω,因此輸入端的電流可假設為零。
2.無限小的輸出阻抗(rout=0):理想的運算放大器輸出端為理想的電壓源,無論經過放大器的負載電流如何變化,其輸出電壓皆為定值,即輸出的阻抗為零,然實際值約小於100Ω以下。
3.無限大的開迴路增益(A0=∞):理想的運算放大器最重要之特徵,係於開迴路狀態時,輸入端的差動訊號有無限大的電壓增益輸出,此特性使得運算放大器十分適合於實際應用時採用負回授組態。
4.無限大的共模排斥比(CMRR=∞):理想運的算放大器只能針對v+與v-兩端點電壓的差值有反應,亦即單獨放大(V+ - V-)的部份;對於兩端輸入訊號的相同部分(即共模訊號)將完全忽略不計。
5.無限大的頻寬:理想的運算放大器對於任何頻率的輸入都將以相同的差動增益放大輸出,不因為訊號頻率改變而變動。
實際的運算放大器在使用時,其增益與頻寬皆為有限值,且輸出功率及電壓會受到限制,輸出電壓值將侷限於工作電壓VPOS及VNEG範圍內。由於運算放大器的增益雖為有限值,但其值可高達104 ~ 106,即便輸入端之差動訊號很小,仍會使輸出訊號飽和(Saturation),導致非線性失真,故運算放大器很少以開迴路組態應用在電路系統中,少數用運算放大器做數位比較器(comparator),其比較器之輸出為邏輯準位的「0」與「1」。
3-2運算放大器電路組態分析
現今運算放大器使用上,大多不採用內部增益進行訊號放大功能,而是由其它被動元件提供負迴授(Negative Feedback)組態使用,以避免電路受到運算放大器本身性質影響。利用運算放大器可實作類比控制器(Analog Controller)、濾波器(Filter)與估測器(Observer)等電路架構,然現今已較少採用類比(Analog)方式,多以數位(Digital)方式實現。於自動控制運用中,若已知系統之轉移函數,則可藉由運算放大器電路模擬此系統響應。
運算放大器之工作模式可用方塊圖(Block-diagram)來表示:

則運算放大器之轉移函數為
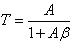
當Aβ>>1時

故可由被動元件A及β之設定,可以決定系統輸入與輸出之間的比值關係。
運算放大器的基本電路組態可細分成反相放大器及非反相放大器兩種,主要是以其增益為負值或是正值做為區別。
1. 反相放大器組態:閉迴路增益為負值

放大增益公式:

公式推導:
此一電路為線性系統,則可將v-與運算放大器連結部份斷開,如圖3-4,以重疊原理求得V- 端電壓值。

令Vout = 0

令Vin = 0

則V- 端電壓值為
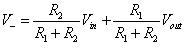
此運算放大器之增益為

由電子學觀點亦可推導此公式。
已知運算放大器輸出值

當開迴路增益 無限大,可得
無限大,可得

當 ,此現象稱為Virtual Ground。
,此現象稱為Virtual Ground。
故可求得流經R1的電流I為
 ,
,
而電流I通過R2到輸出端Vo之關係為

反相放大器系統模擬:
反相放大器控制方塊圖如圖3-5所示,由上述可知反相放大器之增益係取決於外接電阻R1及R2比值。模擬輸入訊號為1V交流電壓,且外接電阻R1=1 KΩ與R2=5 KΩ的條件下,則系統電壓增益值應為-5,由圖3-6之系統響應圖可證實此結果,輸出電壓峰值為輸入電壓之五倍,同時產生180度之相位差現象。
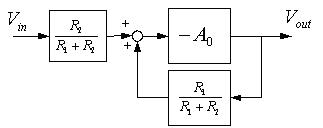
圖3-5:反相放大器控制方塊圖

圖3-6:反相放大器系統響應圖
若改變R1及R2之電阻值,分別為1Ω及5Ω,其電壓增益值同樣應為-5,然而經由模擬得到系統響應圖3-7可直接觀察到,其模擬電路電壓增益值並非-5;係因運算放大器之輸出端具有輸出阻抗的存在,當外接電阻之值夠大時,此輸出阻抗可忽略不計,但若外接電阻值偏低時,則輸出阻抗便會對結果造成影響。
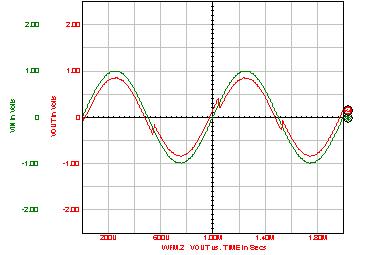
圖3-7:反相放大器系統響應圖
固定R1電阻值為1kΩ,改變R2 電阻值由1kΩ至17kΩ,則最大電壓增益值為-17,觀察其系統響應圖3-8可發現,其輸出電壓增益具有飽和極限值,於此例中約為±14V,此電壓即為運算放大器之工作電壓VPOS及VNEG之值,導致電壓增益受限。於實際電路使用中,則可適當的控制輸入工作電壓值,達到期望的輸出電壓範圍,如圖3-9所示,若僅需正值輸出電壓,則可將工作電壓VNEG之值改為0V輸入,即可達到此一目的。

圖3-8:反相放大器系統響應圖

圖3-9:反相放大器系統響應圖
理想之運算放大器具有無限大的頻寬,然而實際電路中仍為一有限值,可經由模擬頻繁響應圖3-10得之,當輸入電源頻率太高時,其電壓增益會嚴重衰減,故系統實際頻寬約為178kHz。

圖3-10:反相放大器頻繁響應圖
2. 非反相放大器組態:閉迴路增益為正值

圖3-11:非反相放大器電路示意圖
放大增益公式:

公式推導:
推導方法與反相放大器相同,將輸入端與運算放大器連結部份斷開,如圖3-12,分別求得V- 端及V+ 端電壓值與Vin 端及Vout之間的關係式。

圖3-12:非反相放大器截斷示意圖
則V- 端電壓值為

則V+ 端電壓值為

此運算放大器之增益為

以電子學觀點推導此公式。
已知運算放大器輸出值
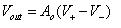
當開迴路增益 無限大,可得
無限大,可得
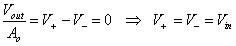
計算通過電阻R1之電流I

再計算通過電阻R2之壓降,可得

反相放大器控制方塊圖如下

圖3-13:反相放大器控制方塊圖
3-3運算放大器之應用
反向放大器與非反向放大器之應用係運算放大器電路之基本組態,其它如積分器、微分器、加法器、電壓隨耦器及差動放大器等,可視為基本組態的延伸應用,以下將各別介紹。
積分器:
將反相放大器組態外接電阻R2部分改以電容連接,如圖3-14,即為電路積分器。其放大增益公式是以電容值1/Cs取代電阻值R2,即可得到。

圖3-14:積分器
以電路方式說明積分器之工作原則,主要係受到電容作用之影響,因電容電壓受到電流Ic與時間t的影響

而電流Ic即為輸入電源Vin經過電阻R1的電流值,為一固定值,導致電容電壓呈線性變化

而電容一端接於運算放大器輸入端,另一端接於輸出端,將使輸出端電壓值為輸入端電壓隨時間變化,並以Ic/C之負斜率下降趨勢。
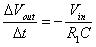
微分器:
若改為將反相放大器組態外接電阻R1部分以電容連接,如圖3-15,即為電路微分器。則其放大增益公式同樣是以電容值1/Cs取代電阻值R1,即可得到。


圖3-15:微分器
由電路上來看,此時電容電壓即為輸入電壓Vin,流入電阻R2的電流為電容電流Ic,則運算放大器輸出端電壓為

又電容電流Ic會受到時間t影響

則輸入與輸出間的關係為

加法器:
由於反相放大器電路為線性系統,故可將輸入端線性疊加後得到輸出端電壓,因此放大增益公式亦是將各輸入電壓與其電阻組合比例疊加起來,如圖3-16。其中各輸入端之電阻組合比例又稱為加權係數,用以表示輸入端影響之比重。


圖3-16:加法器
電壓隨耦器:
電壓隨偶器又稱緩衝放大器(Buffer Amplifier),為非反相運算放大器之特殊運用,如圖3-17,係將輸出電壓直接回授至反相輸入端,此時回授電路增益為1,輸出電壓大小與相位皆與輸入相同,其主要的應用特點在於輸入阻抗值極高,導致輸入電流值趨近於零,但輸出阻抗值卻極低,可供應大的負載電流,適合用於信號源及負載電源之間的緩衝放大器。
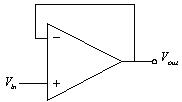
圖3-17:電壓隨耦器
差動放大器:
簡單的說,即是一種將兩輸入端電壓的差以一固定增益放大於輸出端的電路,如圖3-18所示,將V+及V-的電壓差,乘上運算放大器增益A0之後輸出。
V+及V-的值可由重疊原理求得
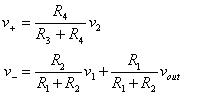
則輸出為


圖3-18:差動放大器
3-4運算放大器應用之實例分析
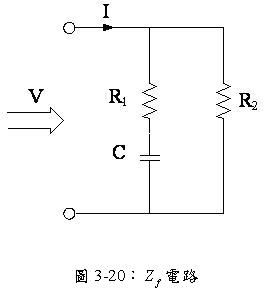
以下將探討一實際的反相放大器電路,如圖3-19,求其轉移函數及系統頻率響應波德圖(Bode Diagram)。

圖3-19:反相放大器電路
代入反相放大器增益公式
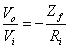
求解,其電路如圖3-20所示,此為一RC電路,則可推測其模態如下
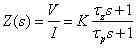
當輸入頻率為零( )時,電容阻抗為無窮(
)時,電容阻抗為無窮( ),則電容為開路狀態,則
),則電容為開路狀態,則

當輸入頻率為無窮( )時,電容阻抗為零(
)時,電容阻抗為零( ),則電容為短路狀態,則
),則電容為短路狀態,則
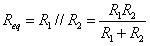
令輸入電壓為零( ),此時電容會經由最小阻抗路徑放電至輸入端
),此時電容會經由最小阻抗路徑放電至輸入端

令 ,則電容會放電,且電流僅於電路內部迴路中流動,而不流入輸入端中
,則電容會放電,且電流僅於電路內部迴路中流動,而不流入輸入端中
求得上述參數解後,可得

反相放大器增益可得
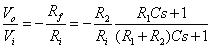
故此反相放大器頻率響應相關參數可知

可繪製出反相放大器頻率響應波德圖,如下

圖3-20:反相放大器波德圖
將實際電阻及電容參數代入,可得


圖3-21:反相放大器波德圖
3-5總結
本章節主要介紹運算放大器的原理與應用,以藉由電子電路裝置以模擬真實系統反應。然而,目前的系統模擬皆採用軟體,如MATLAB等來執行,但在實際的電路應用設計中,為了不佔用軟體計算的資源,部份處理仍可用硬體電路來完成,如各類濾波器等,運算放大器的使用仍然相當普遍,其重要性並不受到軟體能力的增加而減少,善用運算放大器將有助於控制效能的提升。


 留言列表
留言列表
 {{ article.title }}
{{ article.title }}