永磁馬達實務系統架構分析－路昌工業股份有限公司

永磁馬達實務系統架構分析

本文將以能量型式解析永磁馬達特性參數，並導入馬達實際損失[1]，重新架構永磁馬達系統模型。

已知馬達為電能與動能間的轉換機構，永磁馬達實際能量運作程序如下：輸入電能流經馬達導電線圈，藉由電磁效應轉換為磁能，利用導磁材料傳遞，並與馬達內部永久磁鐵交互作用，運用磁性力同極相斥異極相吸特性，於馬達轉子上形成相對運動，產生機械動能輸出，如圖1所示。由此可知，永磁馬達系統具有電氣、磁場及機械三種能量形態。

由熱力學第二定律可知能量於傳輸與轉換過程中，一定會有損失產生，迫使能量無法百分之百傳遞。有鑑於此，永磁馬達可分為電能損失、磁能損失及機械損失三大類別；需將實際損失參數納入永磁馬達系統中，以建立具實務考量之永磁馬達數學模型。

1 永磁馬達標準模型

已知永磁馬達具有三種能量形式存在，分別為電能、磁能及機械能；然而，標準解析方式仍將永磁馬達定義為電能輸入轉換為動能輸出之裝置，如圖2為永磁馬達標準模型系統。

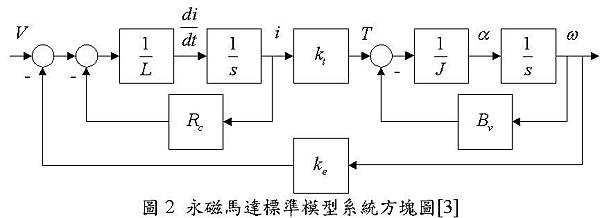
圖2所包含之永磁馬達數學關係式可拆解為兩部份；式(1)為電能部份之電氣方程式，式(2)則為動能部份之機械方程式。

其中V為輸入電壓、i為輸入電流、R_c為線圈電阻、L為線圈電感、k_e為永磁馬達反電動勢常數、ω為馬達轉速。

其中T為轉矩、k_t為永磁馬達轉矩常數、B_v為黏滯係數。

由圖2可觀察到，輸入電壓V到電流i之間即為馬達電氣參數，標準永磁馬達系統僅考慮到線圈電阻R_c所產生之損失；輸出轉矩T到轉速ω之間為機械參數，僅加入黏滯係數B_v之影響；介於電氣及機械參數之間即為磁能參數，僅包含轉矩常數k_t與反電動勢常數k_e，並無描述任何損失。由此可知，永磁馬達標準模型對於損失考量並不完善，無法表達真實的永磁馬達系統，為理想化模型。

2 永磁馬達損失分析

為了將永磁馬達實際損失納入系統中，並藉此重新定義永磁馬達數學模型，需先針對永磁馬達各種損失情況進行解析。已知永磁馬達損失可歸類為電氣、磁場及機械三大部份，再將其細部劃分後，可整理為以下損失：電壓降損、銅損、磁滯損、渦流損、摩擦損、黏滯損及風損。

2.1 電壓降損

電壓降損屬於電氣損失的一種，係馬達電源連接線及換相器所造成的；如圖3所示，馬達需藉電源連接線及換相器傳遞電能至馬達線圈。由於馬達線圈具有電阻值，而電源連接線及換相器亦存在電阻值；由電路學可知，兩電阻串聯會產生分壓效果，導致馬達線圈受到電壓降影響，意即馬達線圈實際跨壓低於輸入電壓值。其計算公式如下

其中V_d為電源連接線及換相器所消耗之電壓值、R_d為電源連接線及換相器之電阻值。

2.2銅損

銅損亦為電氣損失的一種，係指電流通過導電材質時，因材質阻抗所引起之電能傳輸損失，於電路學中稱為導通損失；其來源為馬達線圈電阻，線圈實體如圖4所示。因馬達線圈一般採用具有較低阻抗值的銅作為導電材料，故馬達導通損失皆直接稱為銅損。其計算公式如下

P_c = i²R_c (4)

其中P_c為銅損損失功率。從圖2可知，永磁馬達系統模型中並無標示功率項；為將銅損導入系統方塊圖中，將式(4)重新表示為電壓與電流關係

其中V_C為馬達線圈跨壓值。

2.3 鐵損

鐵材為最熟知的導磁材料，故口語上常稱馬達導磁材料為鐵心；實際應用上，大多選用具有高飽和磁通密度及低損失的矽鋼片作為馬達導磁材料，矽鋼片實體如圖5所示。導磁材料所產生之損失統稱為鐵損，包括磁滯損及渦流損兩種，皆為磁能於導磁材料內傳遞及轉換時所造成之損失。

2.3.1磁滯損

任何能量於傳輸及轉變過程中，一定會有損失，磁能亦不例外；磁滯損係導磁材料原子結構受到外部磁場變化時，重新排列為磁性方向所需耗損能量。磁滯損計算公式如下，並將磁場變換頻率改以馬達轉速表示之

其中P_h為磁滯損損失功率、k_h為導磁材料磁能性質參數、f為磁場變換頻率、B_m為導磁材料磁通密度、N_m為馬達極數。為納入永磁馬達系統中，式(6)重新表示為轉矩與轉速關係如下

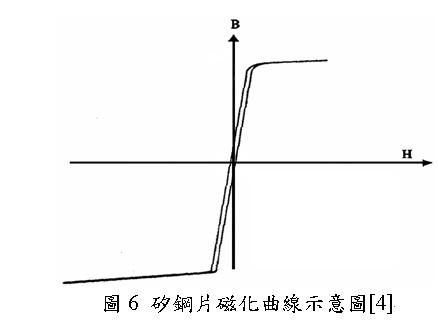
其中T_h為磁滯轉矩。馬達選用矽鋼片作為導磁材料，除了能容納更高的飽和磁通密度外，其材料特性亦具有狹窄的磁滯區域，如圖6所示，兩條磁化曲線間隔範圍極為狹長，使得矽鋼片可快速轉換磁場極性並降低磁滯損。

2.3.2渦流損

渦流損亦為導磁材料所產生之損失，屬於磁能損的一種；係因馬達旋轉換相時，瞬間磁場變動，於導磁材料內產生感應電流流動，而造成損失。計算公式如下，將磁場變換頻率改以馬達轉速表示

其中P_e為渦流損損失功率、k_ec為導磁材料電磁性質參數、d為導磁材料厚度、ρ為密度。將式(8)重新表示為轉矩與轉速關係如下

其中T_e為渦流轉矩、B_e為渦流係數。

2.4 摩擦損

摩擦損為機械損失的一種；當物體於行進間，與其它事物接觸面上會產生一方向相反的力，對移動方向之力進行抵抗，即為摩擦損失，如圖7所示。

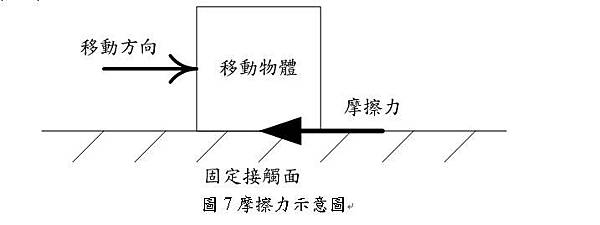
摩擦損又可細分為靜摩擦損及動摩擦損兩種；靜摩擦損係描述物體剛開始移動時，須先施較大的力，克服接觸面之靜摩擦力，方可開始移動；當物體持續行進後，接觸面上依然存在一大小固定的摩擦力，即為動摩擦力。圖8為瞬間摩擦力變化示意圖，剛啟動時有一較大的靜摩擦力F_s，運動速度增加至靜摩擦力存在之最大速度v_s後，僅剩一較小的動摩擦力F_c。其數學表示式如下

其中F_f為摩擦力、v為速度。將式(2.11)之力轉換為轉矩與轉速表示如下

其中T_f為摩擦轉矩、T_c為動摩擦轉矩、T_s為靜摩擦轉矩、ω_s為靜摩擦轉矩存在之最高轉速。

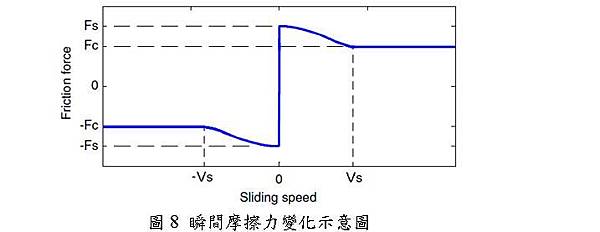
理論上，摩擦力會受到速度參數影響，但影響速度範圍非常小，僅在開始移動瞬間內有顯著差異；而在本研究之量測系統應用上，待測馬達係快速運轉至高速區段，此時僅受動摩擦力影響，故於馬達損失分析中，可將摩擦力視為與速度無關之固定損失。則式(11)改寫如下

T_f =T_c (12)

2.5 黏滯損

黏滯損亦為機械損的一種；當物體在移動時，與流體接觸面上會具有黏滯力，如圖9所示。馬達為轉子受到空氣流體作用，以及軸承潤滑油所造成之黏滯阻力；其特點係黏滯力大小與速度成正比，關係式如下

F_v = B_vv (13)

其中F_v為黏滯力。將式(13)轉換為轉矩與轉速型式如下

T_v= B_vω (14)

其中T_v為黏滯轉矩。

2.6 風損

風損為物體移動方向所受到的正向流體阻力，如圖10所示。於馬達中係受到轉動所引起之空氣流動，因結構空間限制所產生之流場壓力差，進而衍生出來的空氣阻力，故稱之為風損；與速度呈現二次方曲線關係，如圖11所示。

風損計算關係式如下

其中P_w為風壓、ξ為風壓係數。將式(15)以力的形式表示如下

其中A為受力面積。將式(16)轉換為轉矩與轉速關係如下

由式(17)及圖11可知，風損與轉速關係為非線性二次方曲線，為導入永磁馬達系統模型，需將式(17)定義為與轉速係一次方關係，即線性化處理。為達到此一目的，於量測系統設計時，需規劃馬達轉速差異不可太大，於較小的轉速變化範圍內，可將非線性視為線性系統[5]，此為線性化處理中常用之技巧。則可將式(17)處理如下

T_w = B_wω (18)

其中T_w為風損轉矩、B_w為風損係數。

3 永磁馬達系統模型建立與定義

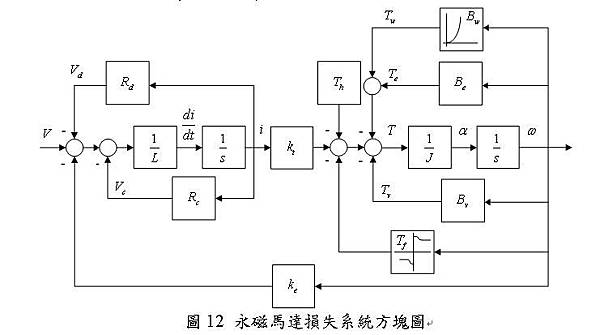
將上述所推導之馬達損失，如式(3)之電壓降損、式(5)之銅損、式(7)之磁滯損、式(9)之渦流損、式(12)之摩擦損、式(14)之黏滯損及式(18)之風損加入圖2永磁馬達標準系統模型中，可繪製出永磁馬達損失系統方塊圖12，即為一具實務損失考量之永磁馬達系統模型。